Бета-коэффициент (β) при анализе акций — что это и как работает
3.3/5 - (12 голосов)
В этой статье вы познакомитесь с коэффициентом β, который чаще всего рассчитывается для акций (но может и для любого актива) при сравнение их волатильности. Также этот показатель помогает рассчитать риски и доходность инвестиционных портфелей.
1. Что такое бета-коэффициент на рынке простыми словами
Бета-коэффициент (β, Beta) — это показатель, который показывает ценовые движения относительно фондового индекса или иного бенчмарка.
Бета-коэффициент впервые предложил Шарп. Он является лишь статистическим показателем. Его исторические данные не гарантируют, что и в будущем соотношения будут такими же.
Это может быть сравнение нескольких портфелей: российских и зарубежных акций, золота или облигационных наборов. Искать зависимость можно между любыми инструментами на бирже.
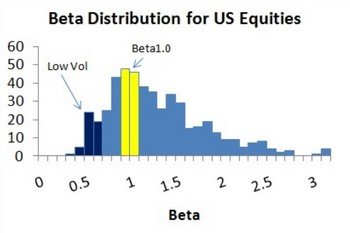
Например, если фондовый индекс вырос на 1% и акция выросла на 1%, то в этом случае β = 1, поскольку движение биржевых котировок полностью копируют индекс. Если же первый вырос на 1%, а второй на 2,5%, то в этом случае β = 2,5, что говорит о том, что акция волатильнее индекса в два с половиной раза. Она будет расти и падать сильнее. Это даёт премию к доходности при бычьем рынке и большие риски при падающем.
Формула бета-коэффициента:
β = Cov(ki,p)/Var(p)
Где:
ki — доходность акции в i-ом периоде;
p — доходность портфеля (чаще всего используется просто фондовый индекс);
Cov (ki,p) — ковариация i-ой ценной бумаги и портфеля (p);
Var (p) — вариация доходности портфеля (p);
Вместо Var (p) в знаменателе часто можно увидеть σ2 (дисперсия портфеля или фондового индекса).
Более подробная формула выглядит следующим образом
Однонаправленное движение, но волатильность акции выше
0 < β < 1
Однонаправленное движение, но волатильность ниже
β = 0
Полностью отсутствует взаимосвязь
β < 0
Разнонаправленные движения рынка и акции
Последний случай редко встречается на рынках. Чаще всего защитные активы в виде золота могут показывать такую обратную корреляцию.
Большие значения Бета свидетельствует о высокой волатильности финансового инструмента по сравнению с рынком. Колебания биржевых котировок могут быть существенными.
Последние исследования показывают, что порой высокие значения бета не дают бонуса в большой доходности. Такова статистика с 1990 по 2010 гг. среди американских акций.
2. Где можно посмотреть коэффициент Бета
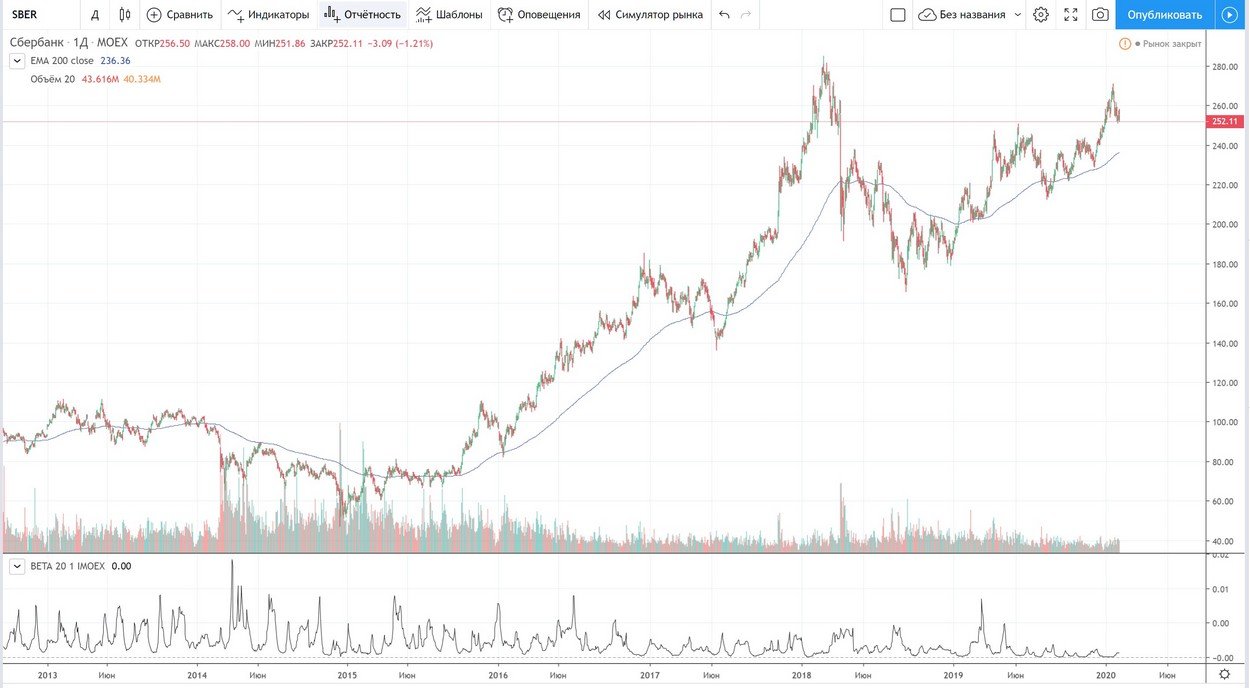
Посмотреть корреляцию наглядно в истории можно на сайте ru.tradingview.com с помощью индикатора BETA, где мы можем также задать с чем сравнивать наш актив. Можно составить самые разнообразные соотношения.
Сбербанк и индекс ММВБ:
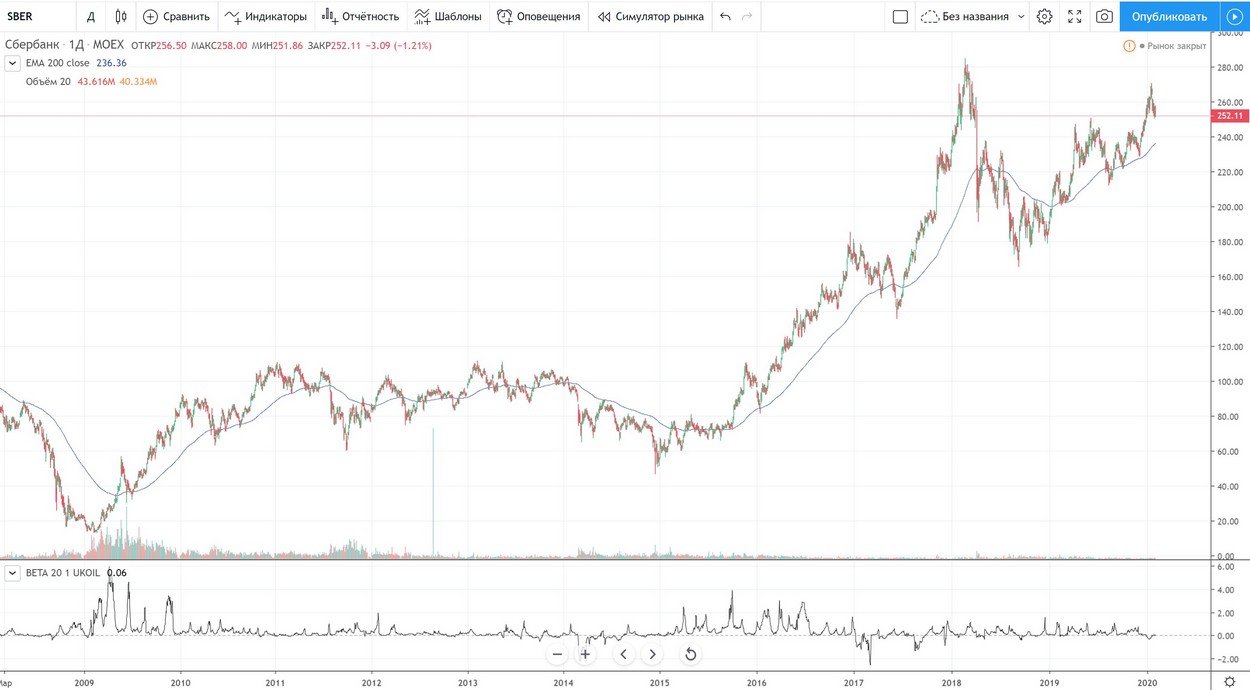
Сбербанк и цена нефти Brent:
С развитием торговли на криптовалютном рынке стали часто сравнивать корреляцию золота и Биткоина. Но как показывает практика зависимость весьма слабая или даже вовсе отсутствует:
3. Коэффициент бета инвестиционного портфеля
Профессиональные управляющие крупными фондами используют коэффициент β для анализа и прогнозирования сбалансированного инвестиционного портфеля.
Коэффициент бета позволяет сделать следующее:
Определить риск отдельного актива (или даже портфеля) относительно бенчмарка;
Составить сбалансированный набор ценных бумаг;
Определить веса отдельных ценных бумаг;
Определить волатильность;
Формула Бета для портфеля:
βп = ∑ (Wi × βi)
Где
βп — коэффициент бета;
Wi — вес i-ого актива;
βi — бета i-ого актива;
Таким образом, можно рассчитать коэффициент бета относительно рынка.
Чтобы максимально сгладить динамику портфеля в него стоит включать акции с положительный и отрицательной бетой. Также стоит всегда иметь какую-то часть в краткосрочных и долгосрочных облигациях. При этом можно составить его из совокупности корпоративных облигаций и ОФЗ.
